One of the common interfaces, perhaps the common interface, of scikit-learn is
fit(X, y), which updates the estimator's internal parameters to fit some data
(potentially based on other hyper-parameters, like say a symbolic model of the
system).
FormaK assesses the model quality and elects model parameters that best fit the data. In order to do that, the FormaK library implements a Kalman filter implementation for quantifying and assessing errors in a structured way. This is similar to some of scikit-learn's functionality (Covariance for example), but adds a stronger model-first capability by integrating a process model (the symbolic model) and "sensors" for translating that process state into the format that data enters the system.
Where this doesn't immediately line up is in selecting the parameters for the
Kalman filter. We have a model of how the system moves through the state space,
we have a state and we have data, but how do we get a fit?
Skip to the Summary if you just want to see how to get this in FormaK
Part 1: What are we fitting?¶
The Kalman Filter provides an additional benefit that I glossed over earlier: it tracks the covariance for the state and, via the sensor models, the covariance quantifies the expected error distribution for each new data point. The error between the predicted measurement and the reading is called the innovation and the score for how that matches the distribution is the Mahalanobis distance.
Normally approach approaches zero; however, for the Kalman filter model we actually want to approach mean zero and standard deviation of 1 when normalized by the expected variance. Zero mean and standard deviation of 1 indicates that we don't have any biases in the model and our assessment of the noise in the system matches the noise in the data.
A loss function for the variance that looks something like this would be ideal:
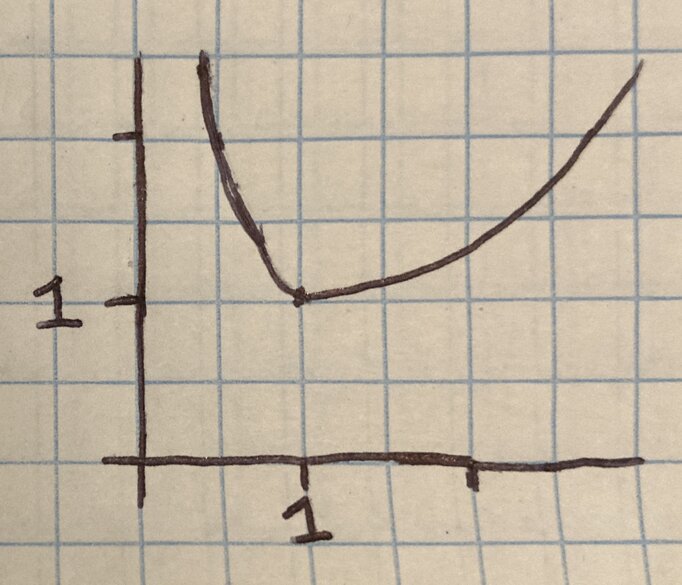
One possible function: ( 1 / x + x ) / 2
As the function approaches 0, the 1/x term dominates and as x grows, x dominates. Together, the functions combine to produce a minima at x=1 (and equal to y=1 with the /2 term).
Part 2: Optimization¶
We have a metric where we can look at our data and understand if it's a good fit or not for the model: the Mahalanobis distance. What's next?
FormaK gets a big leap forward by standing on the shoulders of giants: scipy
provides a general algorithm for optimizing once we have a metric, called
minimize. FormaK provides a function to calculate the metric (would you look
at that, we've got this covered with the Mahalanobis distance) and the initial
state from which to start the optimization.
The initial state isn't quite the state of the Kalman Filter (although that can be a part of it). Instead, to match the optimization problem we're considering (the mapping from choices of noise parameters to innovation outcomes) FormaK uses a state made up of the noise parameters for the model.
Part 3: Results¶
To test out the optimization at a high level, I've set up a simple test case. The data is pretty arbitrary and set around a simple model of position, velocity and acceleration. The code to run the fit looks something like this:
model = python.compile_ekf(
ui.Model(dt=dt, state=state, control=control, state_model=state_model), **params
)
readings = X = np.array([[10, 0, 0], [10, 0, 1], [9, 1, 2]])
# Fit the model to data
model.fit(readings)
fit_score = model.score(readings)
assert fit_score < unfit_score
And the optimization code looks something like this:
# Fit the model to data
def fit(self, X, y=None, sample_weight=None):
dt = 0.1
x0 = self._flatten_scoring_params(self.params)
def minimize_this(x):
holdout_params = dict(self.get_params())
scoring_params = self._inverse_flatten_scoring_params(x)
self.set_params(**scoring_params)
score = self.score(X, y, sample_weight)
self.set_params(**holdout_params)
return score
minimize_this(x0)
result = minimize(minimize_this, x0)
if not result.success:
print("success", result.success, result.message)
assert result.success
soln_as_params = self._inverse_flatten_scoring_params(result.x)
self.set_params(**soln_as_params)
return self
def score(self, X, y=None, sample_weight=None):
state = np.zeros((self.state_size, 1))
covariance = np.eye(self.state_size)
innovations = []
for idx in range(X.shape[0]):
controls_input, the_rest = (
X[idx, : self.control_size],
X[idx, self.control_size :],
)
state, covariance = self.process_model(
dt, state, covariance, controls_input
)
innovation = []
for key in sorted(list(self.params["sensor_models"])):
sensor_size = len(self.params["sensor_models"][key])
sensor_input, the_rest = (
the_rest[:sensor_size],
the_rest[sensor_size:],
)
state, covariance = self.sensor_model(
key, state, covariance, sensor_input
)
# Normalized by the uncertainty at the time of the measurement
innovation.append(
np.matmul(
self.innovations[key],
np.linalg.inv(self.sensor_prediction_uncertainty[key]),
)
)
innovations.append(innovation)
x = np.sum(np.square(innovations))
# minima at x = 1, innovations match noise model
return (1.0 / x + x) / 2.0
This took some tweaking to get right, but the outcome is going from an error score of 1.29 down to 1.00. It's only a couple of data points, so the numbers aren't meaningful, but we can see that the minimization is working to decrease the model error by manipulating the noise parameters.
Summary¶
Under the hood of the fit interface Formak uses an optimization algorithm
working on your behalf to pick model parameters based on your data.
To use this with FormaK, all you have to do is define your model and call fit on your data.
# define physics
physics_model = {
x: x + dt * v,
v: v,
}
# load some data
data = ...
# prepare the model
model = python.compile_ekf(
ui.Model(dt=dt, state=state, control=control, state_model=physics_model), **params
)
physics_model.fit(data)
# profit
From there, you're off to the races working with an optimal model :)
If you want to try this out, check out the
pull request or play with the
branch
sklearn-integration
When you try it out, if you find any bugs or have questions, please
open an issue on Github